矩阵快速幂的介绍及其应用
矩阵快速幂介绍
题目描述
给定 n×n 的矩阵 A,求 A^k。
输入格式
第一行两个整数 n,k 接下来 n 行,每行 n 个整数,第 i 行的第 j 个数表示 Aij。
输出格式
输出 A^k
共 n 行,每行 n 个数,第 i 行第 j 个数表示 Aij, 每个元素对 10^9+7 取模。
1 <= n <= 100
0 <= k <= 10 ^ 12
|Aij| <= 1000
分析:
本质上就是快速幂运算,只是底数变成了一个矩阵。
快速幂运算板子
1typedef long long ll;
2ll mod_pow(ll x, ll n, ll mod){
3 ll res = 1;
4 while(n > 0){
5 if(n & 1 == 1) res = res * x % mod; // 如果指数是奇数则乘上底数
6 x = x * x % mod; // 底数平方
7 n >>= 1; // 指数除二
8 }
9 return res;
10}
由此易得:
矩阵快速幂板子:
1Matrix Pow_Mod(Matrix m){//矩阵快速幂
2 Matrix M;
3 for(int i = 1; i <= n; i++)
4 for(int j = 1; j <= n; j++){
5 if(i == j) M.mat[i][j] = 1;
6 else M.mat[i][j] = 0;
7 }// 结果矩阵, 初始状态是一个单位阵
8 while(p){
9 if(p & 1) M = Mul(M, m); // 如果指数是奇数则乘上底数矩阵
10 m = Mul(m, m); // 底数矩阵平方
11 p >>= 1; // 指数除二
12 }
13 return M;
14}
其中的Mul函数返回两个矩阵相乘的结果:
1Matrix Mul(Matrix m1, Matrix m2){//方阵乘法&取模运算
2 Matrix M;
3 for(int i = 1; i <= n; i++)
4 for(int j = 1; j <= n; j++)
5 M.mat[i][j] = 0;
6 for(int i = 1; i <= n; i++)
7 for(int j = 1; j <= n; j++){
8 for(int k = 1; k <= n; k++){
9 // 相加减取模的运算规律
10 M.mat[i][j] += ( (m1.mat[i][k] % e) * (m2.mat[k][j] % e) );
11 M.mat[i][j] %= e;
12 }
13 }
14 return M;
15}
矩阵快速幂的应用
斐波那契
题目描述:
f(x) = 1 …. (x=1,2)
f(x) = f(x-1) + f(x-2) …. (x>2)
对于给定的整数 n 和 m,我们希望求出:f(1) + f(2) + … + f(n) 的值。
但这个数字很大,所以需要再对 p 求模。
为什么要通过矩阵快速幂来运算斐波那契问题呢,这是因为斐波那契运算的每一项可以用矩阵幂的运算得到,而幂运算又有快速幂运算来快速解决。
为什么可以用矩阵解决?请看下图:
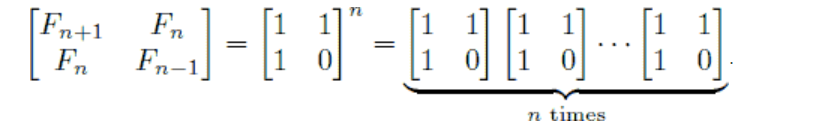
可见斐波那契数列每项都可以由一个矩阵的若干次方得到,而我们又知道可以通过快速幂运算解决开方运算,所以自然可以用矩阵轻松解决!
这里的思想很巧妙:
把一个问题转换为另一个问题,然后就可以通过新的问题特有的且优秀的方法来解决原来的问题。
对于斐波那契数列还有一个重要性质,就是前 n 项和等于 f(n+2)-1,这个结论可以又递推法轻松得到。
代码实现:
1long long n, mod, sum = 0;
2struct Matrix{
3 long long mat[3][3];
4};
5
6Matrix Mul(Matrix m, Matrix m_f, int t) {//矩阵乘法 m*(m_f或m)
7 Matrix M;
8 for(int i = 1; i <= 2; i++)
9 for(int j = 1; j <= 2; j++)
10 M.mat[i][j] = 0;
11 for(int i = 1; i <= 2; i++)
12 for(int j = 1; j <= t; j++)//t==1时得m_f, t==2时得m
13 for(int k = 1; k <= 2; k++) {
14 M.mat[i][j] += (m.mat[i][k] % mod) * (m_f.mat[k][j] % mod);
15 M.mat[i][j] %= mod;
16 }
17 return M;
18}
19
20long long Pow_Mod(long long num) {//矩阵快速幂
21 Matrix m, m_f;
22 m.mat[1][1] = m.mat[1][2] = m.mat[2][1] = 1; m.mat[2][2] = 0;
23 m_f.mat[1][1] = m_f.mat[2][1] = 1;
24 // 结果矩阵 初始化为 [F2; F1] 求n次 -> [Fn+2; Fn+1]
25 // 只需计算2个,降低复杂度
26 while(num) {
27 if(num & 1) m_f = Mul(m, m_f, 1);
28 m = Mul(m, m, 2);
29 num >>= 1;
30 }
31 return m_f.mat[1][1];
32}
33
34int main() {
35 scanf("%lld%lld", &n, &mod);
36 sum = Pow_Mod(n) - 1; // f(1)+...+f(n) = f(n+2)-1
37 printf("%lld", sum % mod);
38 return 0;
39}